An Elliptic Curve and Big Numbers
Suppose you want to find a positive integer solution to
\[ \frac{a}{b+c} + \frac{b}{c+a} + \frac{c}{a+b} = 4\]
Trying a few numbers, up to 10, or 100, or even 1,000,000,000 reveals no solutions... so are there any?
Well, trying a few small numbers without asking for positive solutions might be encouraging. For example, \((a,b,c) = (11, 4, -1)\) is a solution, as \(\frac{11}{3} + \frac{4}{10} + \frac{-1}{15} = 4\). So is \((a,b,c) = (11, 9, -5)\), since \(\frac{11}{4} + \frac{9}{6} + \frac{-5}{20} = 4\) too. These actually give you infinitely many solutions, since if \((a,b,c)\) is a solution, then so is \((2a,2b,2c)\) or actually \((ra,rb,rc)\) for any integer \(r\). After all, \(r\) just cancels out completely.
This idea means that actually it's enough to look for a rational solution (with \(a,b,c\) all positive rational numbers) since we can always multiply through by a common denominator to get some integers. It also means that it's really a two-variable problem - if \(c\) isn't zero, we can divide both \(a\) and \(b\) by \(c\) to get an equation with \(c=1\).
One other observation: if we multiply the whole equation by \((a+b)(b+c)(c+a)\), we get a neat polynomial equation involving only sums and products of powers of \(a,b,c\):
\[ a(a+b)(c+a) + b(a+b)(b+c) + c(c+a)(b+c) = 4(a+b)(b+c)(c+a)\]
or
\[ a^3 + b^3 + c^3 - 3(a^2b + b^2c + c^2a + ab^2 + bc^2 + ca^2) - 5abc = 0\]
This is a homogeneous degree 3 polynomial - which just means every term has three terms from \(a,b,c\) all multiplied together - with all rational coefficients.
We already know that it has rational solutions (\((a,b,c)=(11,4,-1)\) for example), and in fact this is a special object called an elliptic curve over the rationalS. If we use the trick above to scale down to \(c=1\), we can draw all the solutions:
This is the curve of solutions to the cubic equation
\[ a^3 + b^3 + 1 - 3(a^2b + b^2 + a + ab^2 + b + a^2) - 5ab = 0\]
Highlighted in red are the positive solutions - and we want to find a rational point on this red stretch of curve.
Chord and Tangent Games
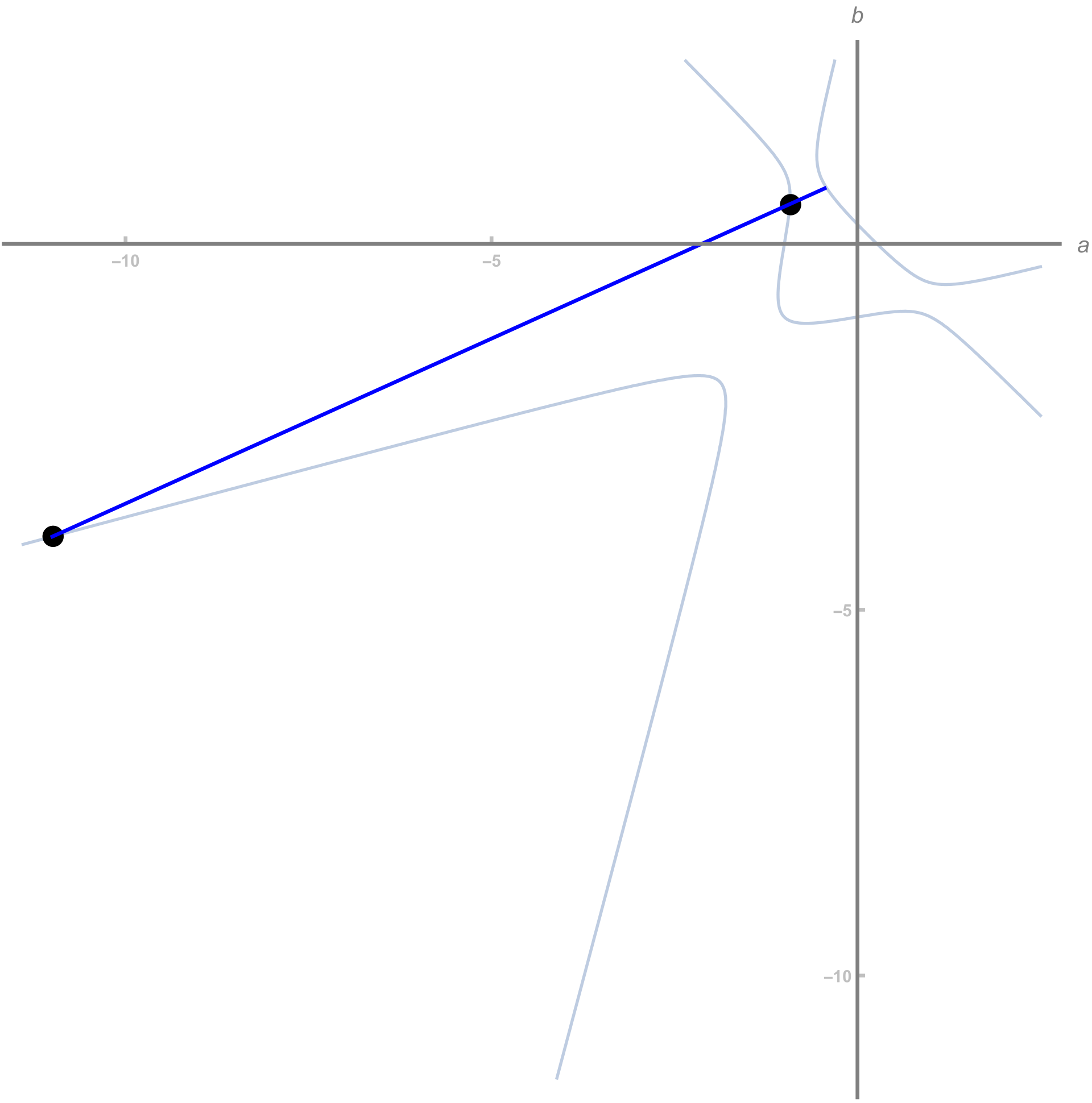
Well, we know some rational points, like \((-11,-4)\) (which comes from dividing \((11,4,-1)\) through by \(-1\)). It would obviously be great if we could find a way to put our hands on new rational points given some old ones.
Drawing Chords
So suppose you have an equation like the one for \(a\) and \(b\) that we wrote above, and two solutions at rational points \(P = (a_P,b_P)\) and \(Q = (a_Q, b_Q)\). What could we try to do to find a new point? One interesting idea is to draw the line connecting these two points together. That is a line with equation
\[ b - b_Q = \frac{b_P - b_Q}{a_P - a_Q} \left( a - a_Q \right)\]
which has rational slope and intercepts, so any time \(a\) is rational on this line, so is \(b\). That's an interesting property. So we could instead write this as
\[ b = ra + s\]
where \(r\) and \(s\) are rational numbers:
If you substitute this into the cubic equation \(a^3 + b^3 + 1 - 3(a^2b + b^2 + a + ab^2 + b + a^2) - 5ab = 0\) we'll get a new cubic equation involving only \(a\) and a bunch of rational numbers. At first, it will be a mess like
\[ a^3 + (ra + s)^3 + 1 - 3(a^2(ra + s) + (ra + s)^2 + a + a(ra + s)^2 + (ra + s) + a^2) - 5a(ra + s) = 0\]
but at the end of the day, it will simplify down to a standard cubic equation \(\alpha a^3 + \beta a^2 + \gamma a + \delta = 0\), or, dividing by \(\alpha\),
\[ a^3 + \beta' a^2 + \gamma' a + \delta' = 0\]
What is this equation telling us? Well, every value of \(a\) that satisfies it is the horizontal coordinate of a point lying on the line \(b = ra + s\) and the original cubic equation of the elliptic curve. So it matches up with an intersection point of the two curves. But we know two of those: the points \(P\) and \(Q\), with coordinates \(a_P\) and \(a_Q\). So these must be two solutions of our new equation. Now a cubic with two real roots must have a third (which might be a double root - we'll come back to that!) and so it's possible to write
\[ a^3 + \beta' a^2 + \gamma' a + \delta' = (a - a_P)(a - a_Q)(a - a_{\mathrm{new}})\]
which defines a new point \(a_{\mathrm{new}}\) corresponding to an third intersection of the line and the elliptic curve. But notice that, since the cubic on the left has rational coefficients, and the cubic on the right contains rational numbers \(a_P\) and \(a_Q\), the number \(a_{\mathrm{new}}\) must also be rational! For example, if \(a_P,a_Q\) are not zero, we can expand the brackets on the right and we get an equation
\[ \delta' = -a_P a_Q a_{\mathrm{new}} \qquad \implies \qquad a_{\mathrm{new}} = -\frac{\delta'}{a_P a_Q}\]
that fixes this coordinate in terms of rational numbers. Even better, the formula \(b = ra + s\) tells us that the corresponding \(b_{\mathrm{new}} = r a_{\mathrm{new}} + s\) is also rational!
So given two rational points, we can construct a third! This is definitely progress.
Double Roots and Tangents
We mentioned something special might happen if there's a double root of the equation. When does this happen? Well, this means that we are on the borderline between having 3 real roots and only 1 real root, which happens when the line just touches the elliptic curve - i.e. when it is a tangent to the elliptic curve:
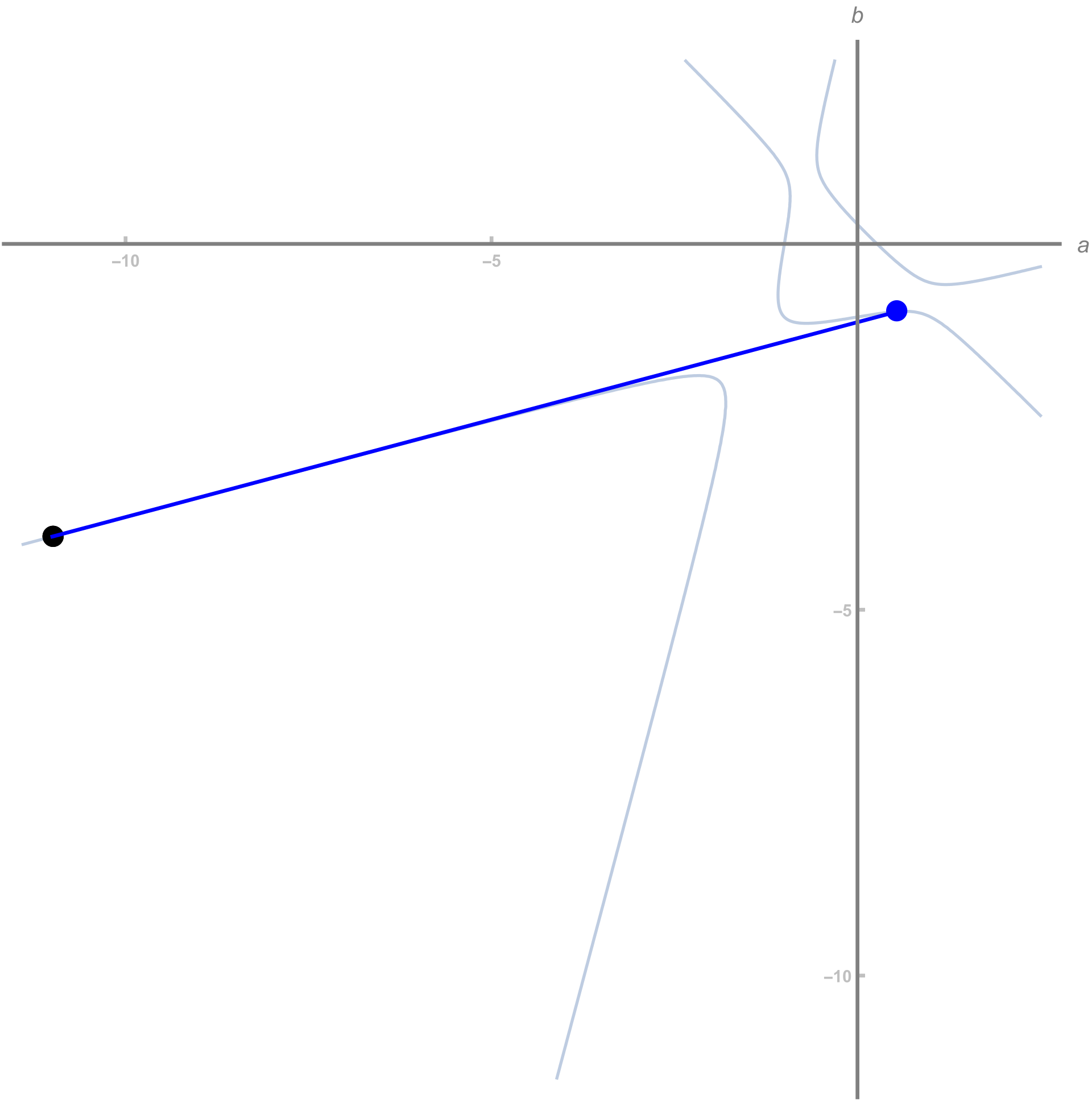
This is actually really useful. If we have a single point on the graph, and we deliberately draw a tangent there, we know that the cubic will now take the simple form
\[ (a - a_P)^2(a - {a_{\text{new}}})\]
TO BE CONTINUED...